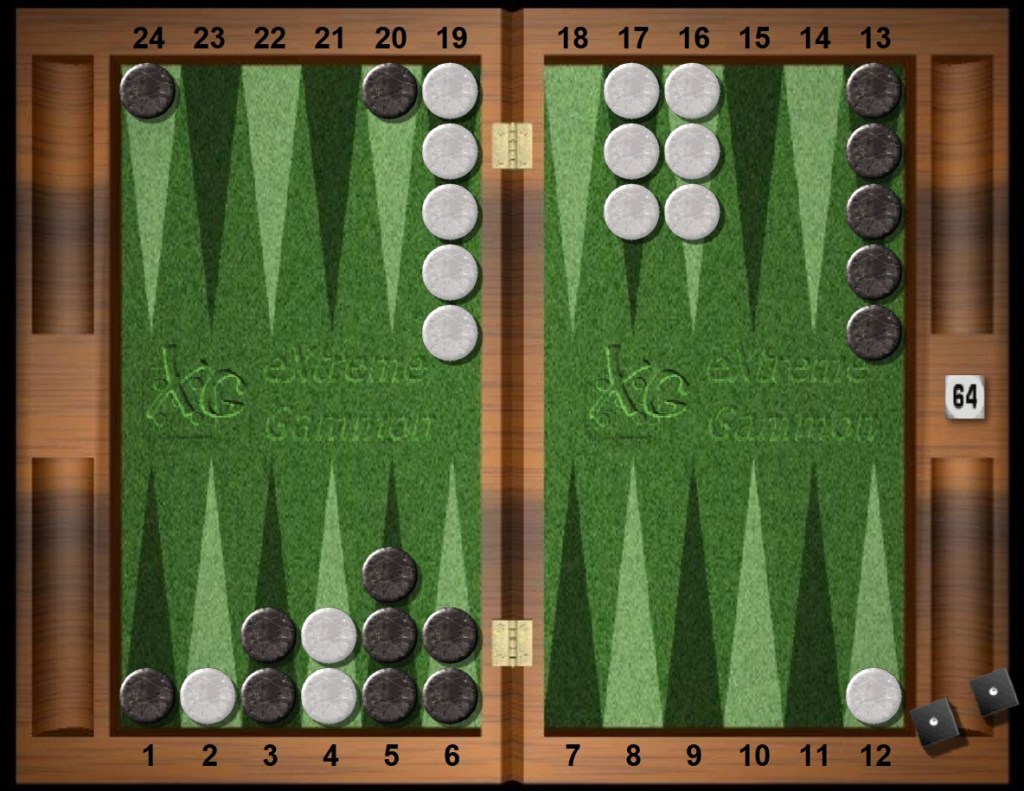
Five point match. White’s match score is two, Black’s zero. Black on roll. Cube action? During the pause, Black considers a double and White considers a take.

A short match with score B:W as 5a/3a, so the baronMET probability of Black (on roll) to win this match is about 3/8.  Of course, Black’s game chances are better than even money.  But game chances are not the same idea as match chances.

What does Sly’s trio of game plans suggest? 

Black has a racing lead of about two rolls. 

Both B and W have some structure, but quite different structures.  Black has the better home board with three home points plus a coverable slot.  Black controls the outfield.  Black currently has mobile backmen but no anchor.  White has a premium anchor, but scant presence in the outfield.  White has no new home points yet but a very menacing block with spares. 

Threats are certainly available to both W and B.  Black has a direct ace shot in the outfield (17 shots total) and a recurring pick-and-pass shot in his home board (2 or 3 shots).  Hence Black is about even money to hit White now.  Black also threatens to make the golden anchor.  White is poised to attack Black, carefully ramping up a blitz in the process.  Considering the disparity between the B and W home boards, the communication between the two black runners seems an asset, with checkers available for counter attack.

Trailing in the match, is this a good double?  Black views his market losers as a subset of his even money hits. 

For money, Black does not have a first cube.  The volatility is quite low, maybe half the initial opening toss, and the market losers are sparse indeed, far less than one-in-ten.  How so?  Make a ballpark estimate of market losers:  Only a Black hit (1/2) and a White dance (1/4) can even be labelled a market loser, and definitely not all of them – hence less than 10%.  Ballpark. Such is the merits of a premium anchor.

Of course White has a Take.  For money White has a take based on the good anchor and sensible chances in any race later, plus the upcoming threats.  The position is only a bit more gammonish than an initial opening toss, which helps the take since White’s gammons now win the match whereas Black’s gammons do not. They only achieve the Crawford game.

At this score, a white drop makes the score 3a/4a where White wins the match 4/7 of the time. 

At this score, a white take and loss makes the score 3a/3a, even chances to win the match.

At this score, a white take and win makes the score 1a*/5a where White wins the match about 5/6 of the time. Crawford game for White.

All this figuring ignores gammons.  That makes the arithmetic simple: Compare drops to takes, and tally the outcomes as odds. Here, White risks-three-to-gain-eleven  {1/14 vs 11/42}  in the match which is a bargain for the substantial game chances of White in this position. Hence White takes the cube. White does win fewer gammons than Black in this position, but those won clinch the match — a deal sweetener worth maybe a 1/6 chance of surviving the match should Black win a gammon.

Too few market losers, no need for more accurate calculations involving gammons.

Without markets losers there is no double. Without enough market losers, there is no double today.

Conclusion:  Black does not have enough market losers to turn the cube yet.  Black needs to create a crisis situation with more market losers before he can double.  ND/T