In a cash game sometimes a position offers two plays about equal in profits but one play is riskier with more losses of single games yet generates more gammon wins. How many extra gammons are needed to offset the additional loss of a single game? In a cash game this currency exchange is well known — two-to-one — but only approximate. In equity it takes a pair of new gammon victories to offset an extra loss of a single game. Consider the position below where the subtleties are explained.

Black has recubed and now converts the situation into a bearoff against the white golden anchor. Black could clear the 6pt immediately with the play 6/4(4). The resulting position is shown below.

White now has little chance to win this game and sometimes will fail to remove any checkers at all, thereby losing a gammon at a 4-cube. Ouch.

Extensive rollouts estimate White’s victories at fewer than four games in ten thousand (0.034%). White owns the doubling cube, but White is even less likely to redouble, only one or two games in ten thousand. It is very rare to win a bearoff race when starting eight rolls behind. In effect, the doubling cube is dead.

Black is likely to gammon White after the clear of the 6pt. The rollouts say Black gammons White in 22.86% of the games played from this position, but never wins a triple game.

Does the currency exchange on gammons recommend the riskier play of taking three black checkers off the board but delaying the clearance of the 6pt? The play 4/0 2/0(2) ? Clearly, Black should win more gammons, but now an eventual toss of Black 51s or 61s might leave a blot, giving White a shot and, with her home board strength, a sudden hit and turnaround victory. These are the more gammons won and the more single game losses under discussion. It begins from the position below.

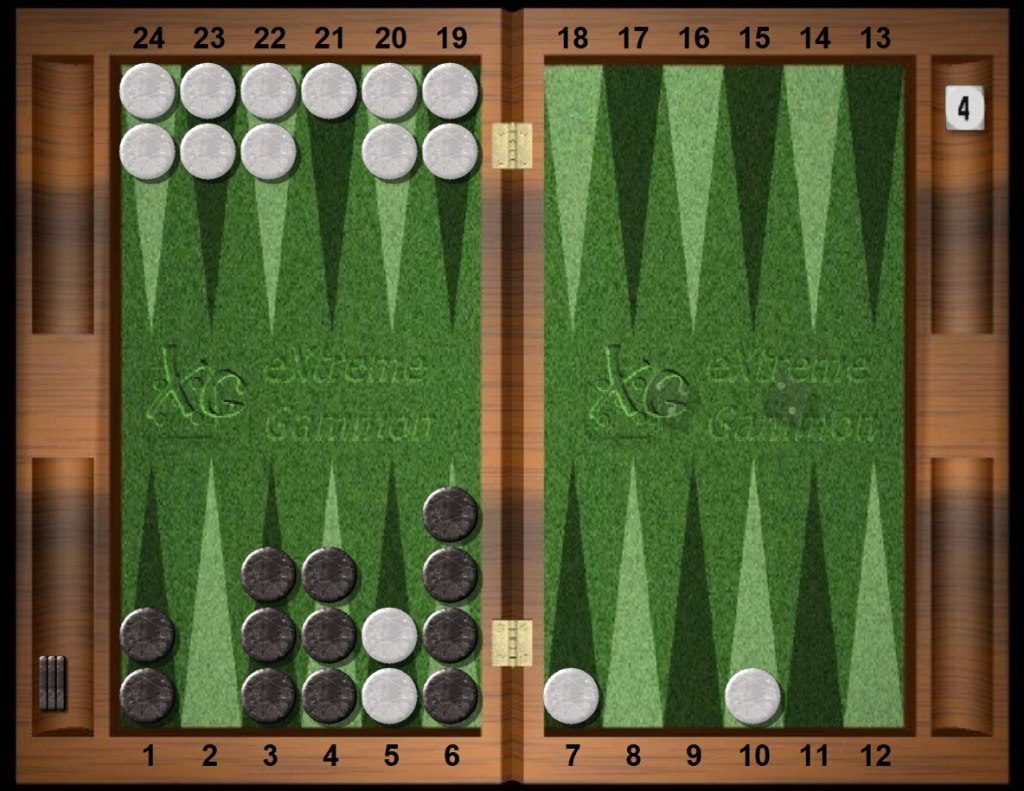
For the play that takes three checkers off, the rollouts claim White wins 2.433% of the time, and Black wins 29.394% gammons, plus an extra “tip” for the triple games after 0.08% of the games.

Now the lawyers get involved, the caveats appear, and the approximations in the classic 2-to-1 currency exchange for gammons then get applied.

First, the Game-Winning Chances (GWC) tallied by the bot during the rollouts are for a dead cube. That means every game in a rollout case is finished. What would be a cube action is asked at each play but stored separately as a different tally.

That doesn’t matter much after the clear of the 6pt. White rarely wins at all, let alone by a recube. The equity of the position without contact is easily computed. For Black let the {total,single,gammon,triple} wins be {W,S,G,B} and for White, {w,s,g,b} from the cubeless rollout tally. The cubeless equity is:

E = S + 2*G + 3*B – s – 2*g – 3*b = 1.2279 dead cube (times four from the 4-cube).

The live cube tally is also 1.2279, since the rare white wins do not happen fast enough to redouble, but as jokers on the final bearoff.

The risky play is a different story. There, the lion’s share of the White wins occur after Black blots and White hits, whether Black dances on White’s home board, or whether Black enters and White hits again. Between Black clearing the 6pt and Black bearing three off, White’s wins go from 0.034% to 2.433%, which increase Black’s losses by 2.4% cubeless. These extra losses thereby demand Black wins 4.8% more gammons. It looks like Black does get the gammon bonanza, from 22.860% to 29.394%, or a 6.5% increase.

But hold on, these numbers ignore the ownership value of White’s cube. In this position, cube ownership is found by the difference between cubeless and cubeful equities for the 3-off play: namely, 1.2461 – 1.2357 = 1.0% which means White wins 1% more games by redoubling.

The last diddly corrections come from first the few triple games Black gets, an extra 0.08% tip, and second the observation that the rollouts say the two plays are not exactly the same equity to begin with, since the safe play is a tiny 0.8% weaker than equal.

Don’t bother sweeping all these numbers together, just realize the two plays are about the same equity but of rather different characters.

As a homework puzzle, which play in the position below is better? No need for rollouts now.

How does cube ownership look now?