A benchmark position must be set up by memory, no exceptions. To remember, a short narrative may be attached to the backgammon situation, where the herald proclaims a royal position with its entourage a chorus of backgammon ideas. Tweets blare the bling: a closed board, a number puzzle.

Black on the roll. Closed home board. Mentally pair the bottom checker on the 1pt with the top checker on the 6pt, the bottom 2pt checker with the top 5pt checker, and so on. The total is six pairs each with seven pips — the 42 pips of a closed board.

How to spread the three remaining spares? The other three checkers (currently in the bathtub) need to be added to the home board. With the spares distributed flat, there are only short standing nails to be hammered down. Coverage numbers on the dice want to spread out in probability, morphing into decisions about spares and stacks. Put three spares on the 6pt? Or on the 5pt? Or below? Suppose Black is ahead in the footrace entering the bearoff. With the three checkers spread anywhere atop the closed board, there are many setups ranging from 60 pips to 45 pips. The situation thus needs constraints.

Constraint #1: No Black checker has yet made it into the bearoff bathtub.

Constraint #2: Exactly 49 pips total.

The magic number in this position will be 49, the average sum of pips upon fair dice after six rolls; not ballpark, exact. The average pips moved in six rolls of the dice: 49. Hence the other three checkers will total seven pips. Not possible with a 6pt spare. A 5pt spare stacks the 1pt (see below).

The next selection of another checker distribution in the home board includes a spare on the black 4pt thus forcing the 1pt-2pt lowball spares (see below).

What is true for a tall stack of five is thereby true for a stack of four checkers and, ipso facto with a sprinkle of reductio ad absurdum and other nonsense, the search collapses to four candidate setups among three spare checkers.

Next, a big stack on the 3pt is possible, with the last spare on the acepoint (see below)

Lastly, a position where the spares are clumped deep (see below):

The spare checkers do a jig but the pip count and the dice rolls both call the tune.

Number puzzle: Three checkers onto a closed board, itself demanding 42 pips. That leaves seven pips for three spares to shuffle around and play with, but always a total of 49 pips. Four candidate positions. Which is best when Black leads in the footrace?

Short narrative: Spares 5pt-1pt-1pt or spares 4pt-2pt-1pt or spares 3pt-3pt-1pt or spares 3pt-2pt-2pt in Black’s closed home board, the pips all tally 49 during the bearoff, and each position a direct mimic of six average rolls, applied to the bearoff. Likely, plus any extra dice rolls to overcome pip wastage while bearing off.

Pip wastage happens during the bearoff for two reasons: (1) a gap number is rolled and unable to bear off a checker or (2) a vacant higher roll is applied to the bearoff of a lower location, thus wasting pips but not scuttling a checker removal.

The chances that the fifteenth checker is off after a mere four rolls requires back-to-back-to-back-to-back high doubles. Then there is the history book after five rolls, after six rolls, after seven rolls, after eight or nine or ten rolls or longer.

Note to self: Obtain the data from hand rollouts at Double Match Point, then bin the data by number (“n”) of game ending rolls into boxes All_Off[n]. White is endowed with the same home board, but a roll behind, by definition. White waits for her turn to roll the dice, after Black rolls and bears off some of his checkers.

Here is the basic position for the hand rollout:

Bonus question: Is that White’s best spare distribution for a comeback win?

The doubling window is quite narrow. The reference take point is pretty enough (see below). Note that the colors have been flipped. White now doubles Black and, with Black stacked entirely on the 5pt, Black can Pass or Take the cube without penalty.

A beautiful position which captures the essence of doubling during the bearoff of a running battle. White’s home checkers are set up for a pipcount of 49, six average rolls. Black’s home checkers are also ready to bear off, but are nearly an average roll behind. Saving every hand rollout and determining who wins after each of three rolls, four rolls, five rolls, six rolls, and so forth will accurately convert the pip lead into the roll lead, available for future use.

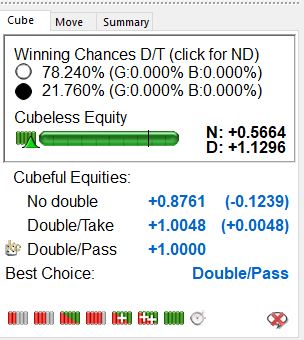
The cube is a Pass by only 5mp after a lengthy rollout of a third of a million cases.

Note to self. Save this position as RTP_496 which parrots the 49/6 average dice roll with the dice variance of (666-1)/36, hints of devilry. Stay tuned for longer rollouts. Then use the probability generating function G(z) to try an analytic assessment to the 3-1 theory.

36G(z) = bz^3 + cz^4 + dz^5 + dz^6 + fz^7 + ez^8 + dz^9 + bz^10 + bz^11 + az^12 + az^16 + az^20 + az^24 where a=1, b=2, c=3 etc See also computer algebra BG_dice. Or perhaps use the central limit theorem to estimate multi-roll variances.