Cash game. Jacoby rule. Black opens with the toss of 54s. Black splits to White’s golden point and shifts the black midpoint spare to the Black 8pt stack.

White replies with the roll of 46s. The other classic opening plays for the roll of 46s are the big split 24/18 13/9 or the straight run 24/14. Here the third classic opening choice becomes best with White making her own 2pt. This play is best for White because White does not want to create extraneous target blots. White really wanted to hit the black blots but cannot. Making the second home board point means White can attack Black on White’s next roll, if possible.

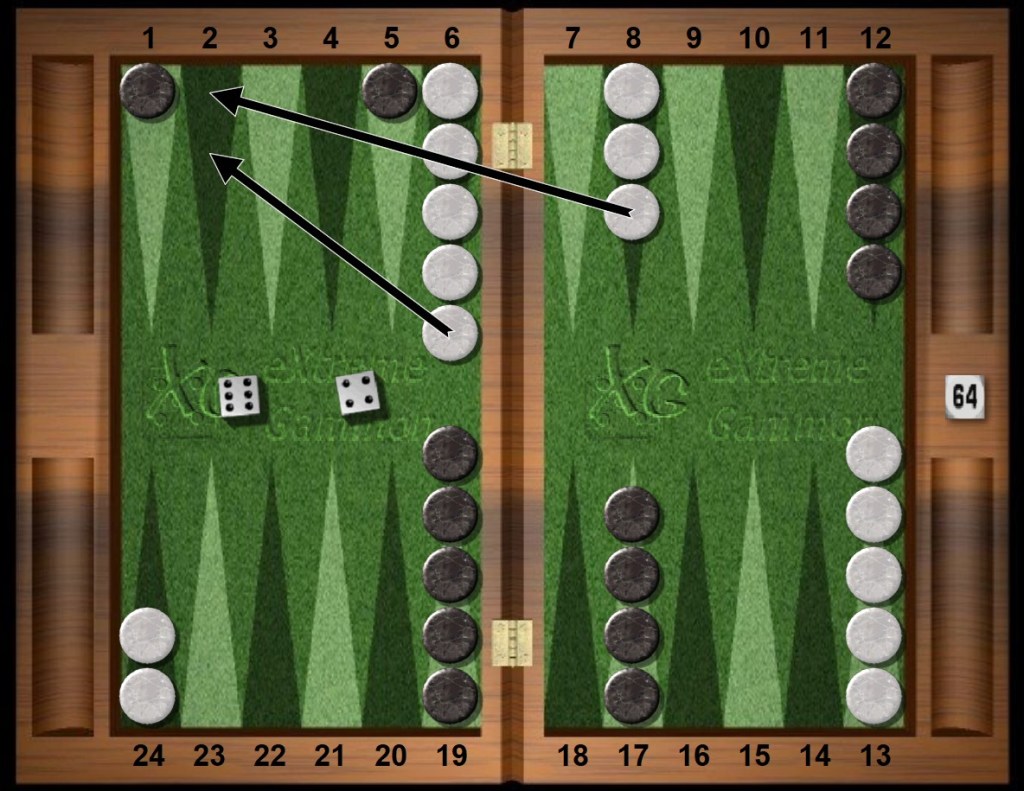
For White to run to her 14pt would be a mistake here, bleeding away the life force of Equity in 50mp drops. White makes the home 2pt.

Black now rolls 63s and advances his forward runner into the relative safety of the black outfield, 20/11.

White rolls double 11s.

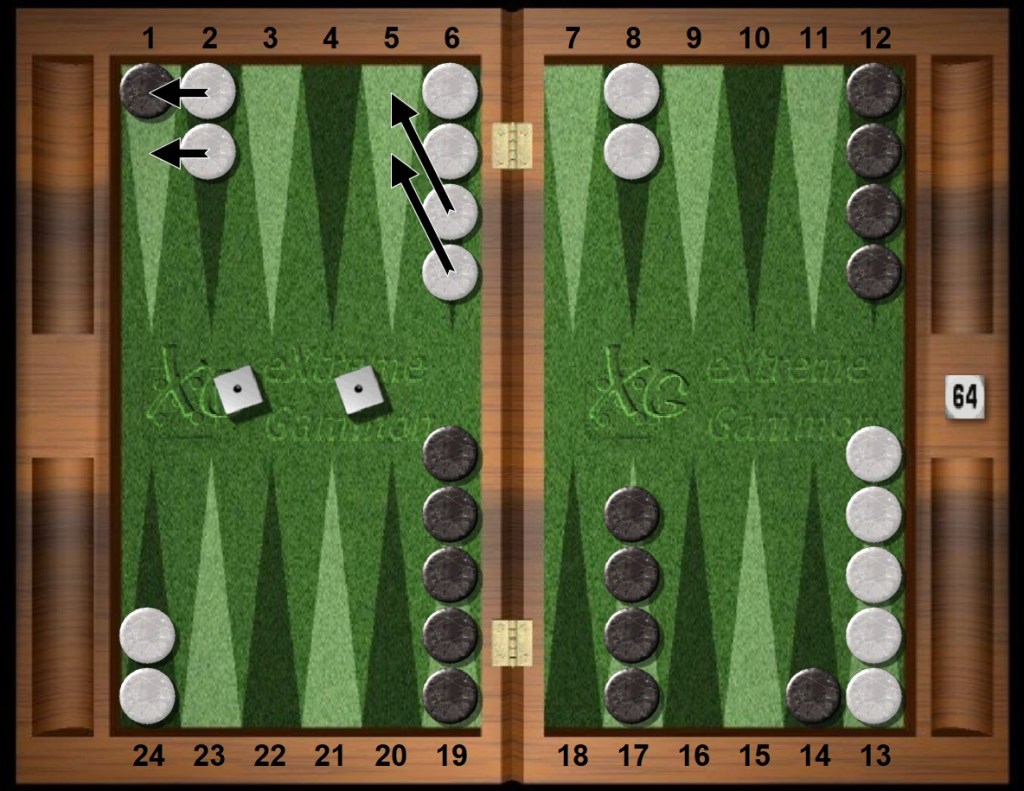
White grabs her golden 5pt and points on the black blot on White’s 1pt. White is now entirely in attack mode.

Black rolls 32s from the bar.

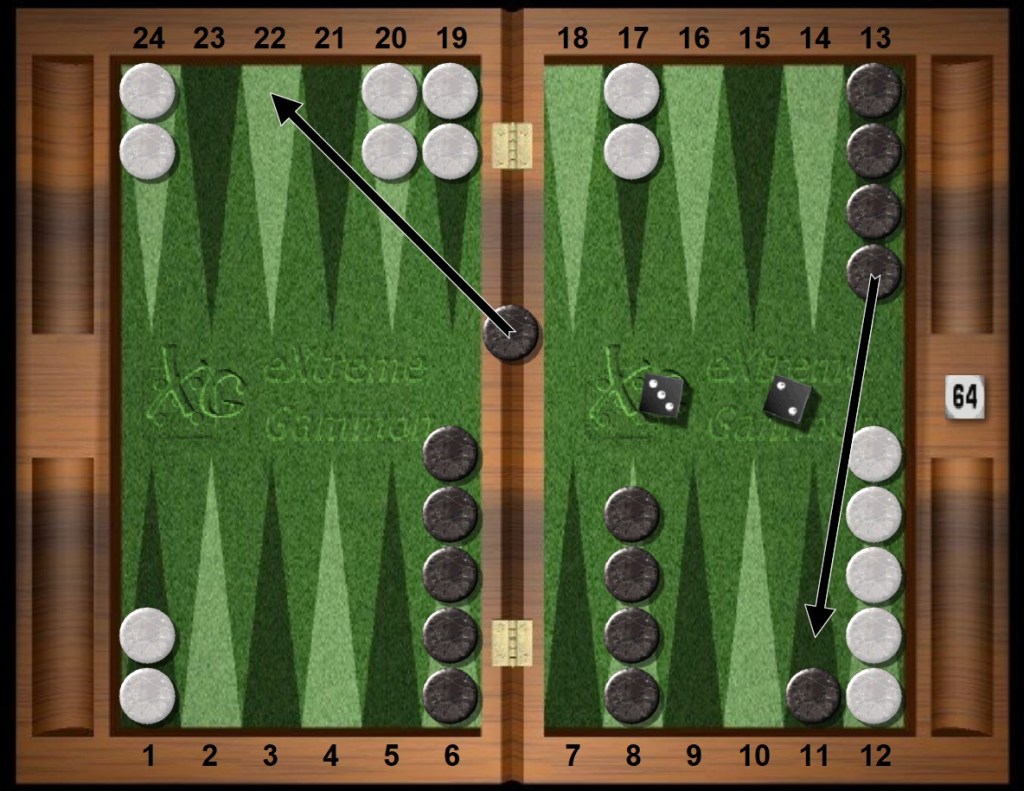
Black rolls 32s from the bar, entering on the 22pt and making the outfield 11pt by covering the other black runner. Black wants to leave blots only in one area of the backgammon board.

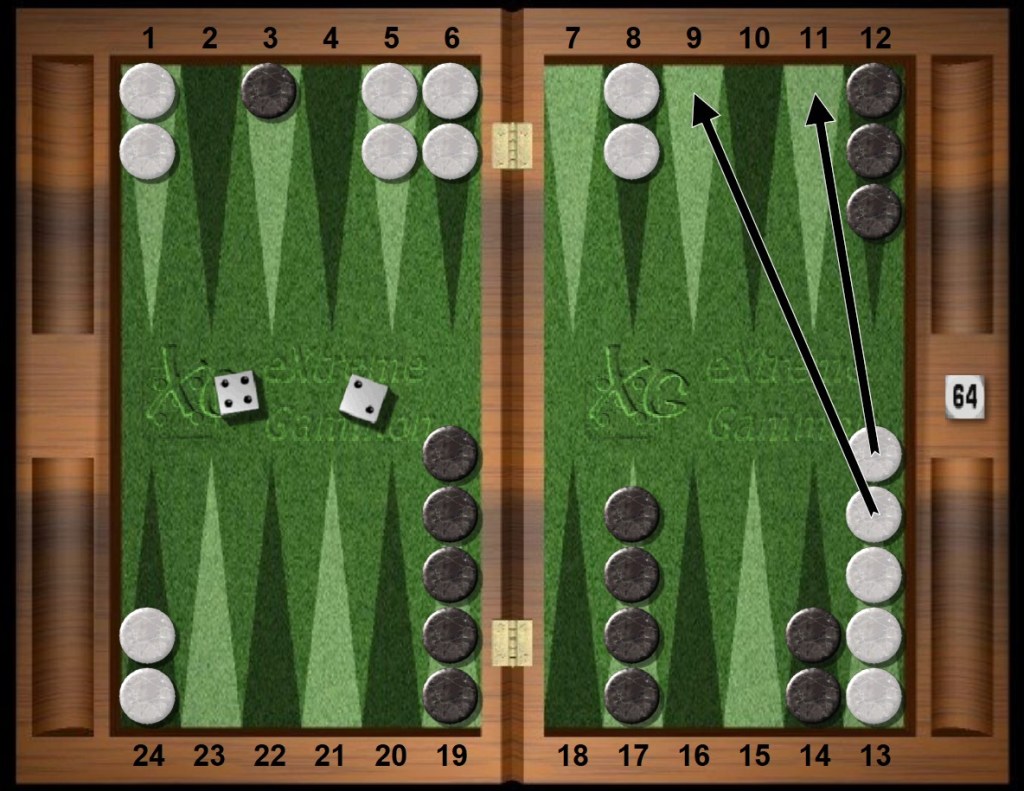
White rolls 24s and unstacks her builders. This leaves a direct shot for Black, but no other play develops White’s position in a positive way.

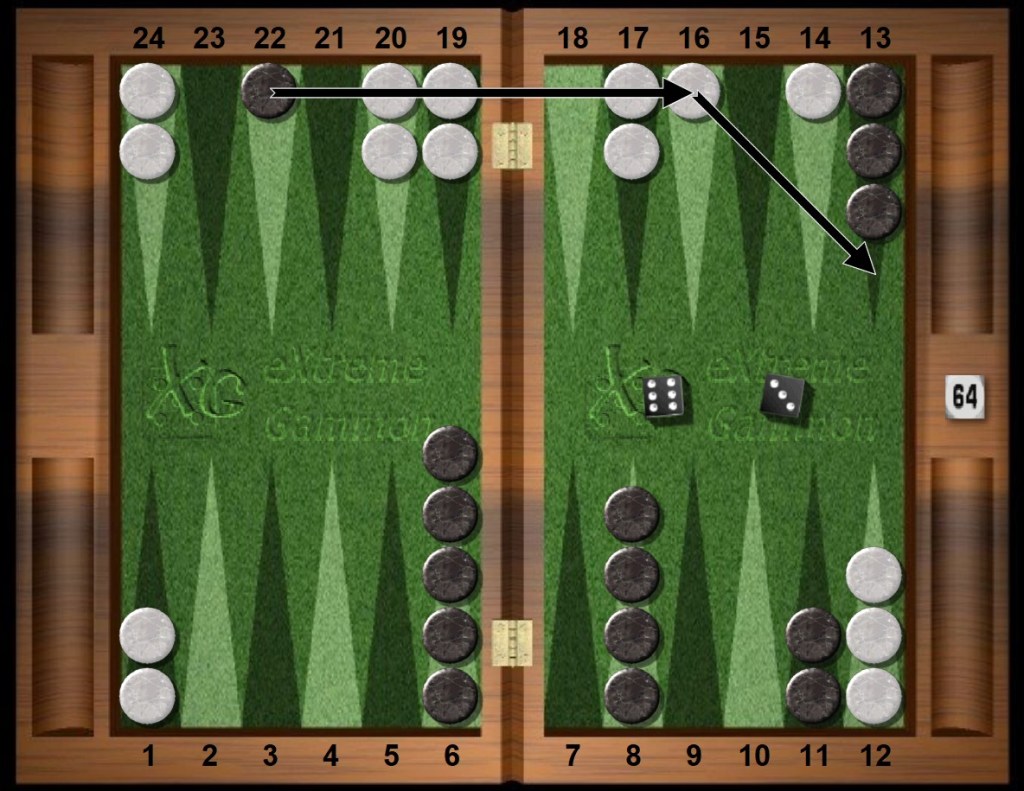
Black rolls 63s, hits the white outfield blot, and continues to the midpoint. Black has a Houdini position, meaning no trapped blots in a running game situation.

White rolls 16s from the bar and continues to start the 18pt.

Black pauses to consider a first cube.

Black has threats on White’s barpoint blot, Black has escaped into a racing structure and leads by more than two rolls. However, a cube without another made point in the home board is typically a double on a promissory note and can easily fizzle. Ugly as it is, White has the better home board and likely will not be blitzed and could even upgrade the anchor to the barpoint.

Black makes the correct decision to wait before cubing. In a cash game the very first moment to double comes in the volatile positions. The more volatile a situation is, the farther Black can edge from the cube canyon awaiting the abyss. Here, the volatility is not particularly high, so Black waits.

Analysis after the game says Black has 267 market losers (in 1296 exchanges) or 20% of the roll exchanges. However, the market losers occur primarily with double 11s, 44s, 66s and often 33s, which occur only about one in nine dice rolls for Black. The volatility of this position is average. Few other roll exchanges are killers.

No new home points for Black. That absence stifles more than just attack, it stifles safe landing posts for the main game plan of running home and bearing off.

No Double.

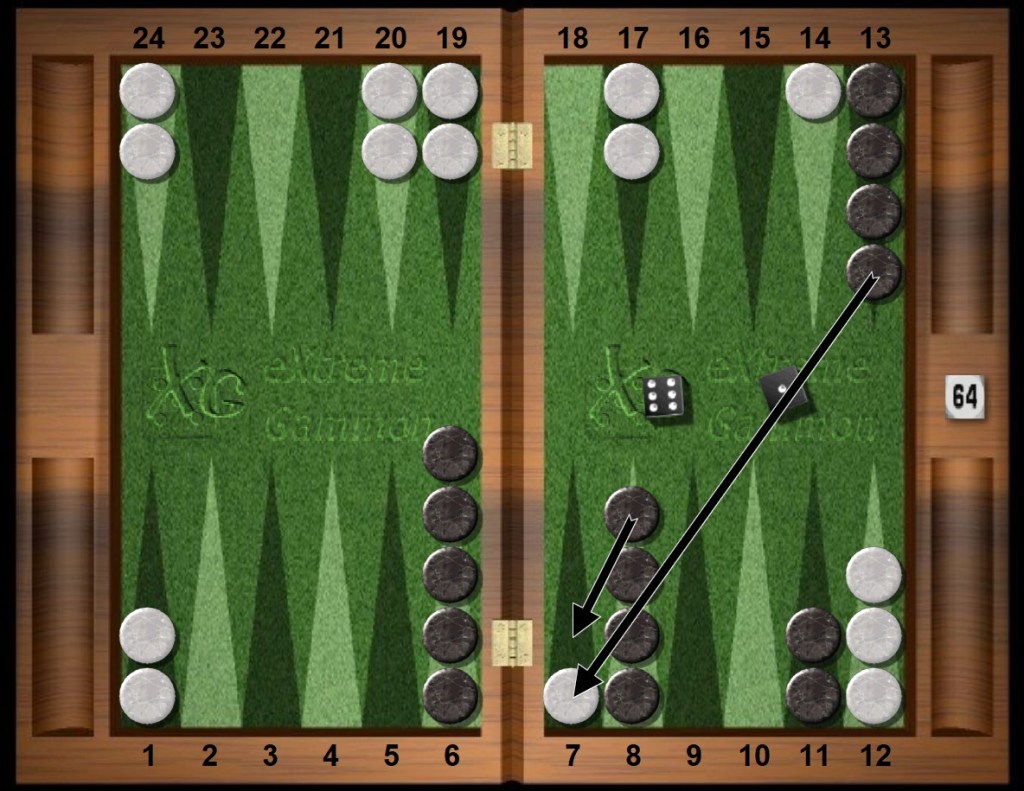
Black does not double and rolls 61s, making the useful barpoint, hitting White off a possible forward anchor and onto the bar dancing.

White enters from the bar with the lackluster roll of 13s, starting the better anchor B/21 (the Black 4pt).

Black is now almost four rolls ahead in the race and has made the blocking 7pt. White still does not have a high anchor. Even though Black has made no new home points, a majority of impending dice exchanges (Black rolls then White rolls) are market losers. In fact, the previous history of Black hits and points then White enters meekly is a realized market loser. Hence:

Black doubles and White passes.

After study of this cube position the conclusion is about half of Black ‘s sequences are market losers from this position. A rare situation where White cannot take even though Black has no new home point.

Rollouts confirm: In round numbers Black wins 3-games-in-4 while White wins 1-game-in-4 and Black wins about four gammons for every gammon White wins. Therefore, no matter how many gammons are for Black’s advantage, the situation carries Black’s equity well above simple 3-1 theory.

D/P