This position came up last week, a juicy racing tip to entice a study group of aging experts. Nowadays, these little scraps of data fling like fireworks through the internet, raining drops of backgammon positions splattered willy and yonder. In truth, to gain the attention of an aging expert, the situation on the board must show a hearty promise of mayhem.

Then it starts. It starts with an utterance. A cry of disbelief. A contralto voice whinges and whistles into an esoteric bafflement. How is this board position even a take, let alone a wait til later to double?

Better have another look at the situation. Again.

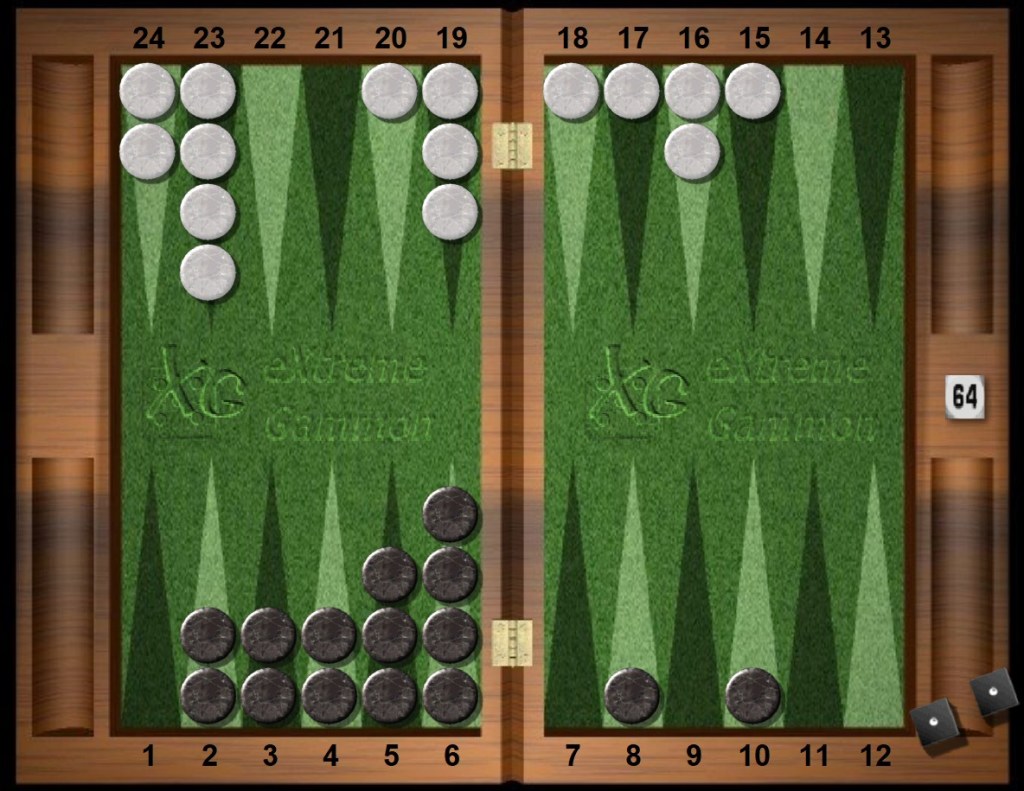
Black to roll the dice. The last two runners are about to be welcomed home, as late crossovers at their own drinking party near the bottom left corner. Modestly, White needs an exquisite pair of high doubles to romp home and boast any similar welcome. Even now, within White’s home board is a tunnel at her empty four and three points. During her run home, most but certainly not all, of those interior white points will be paired, compliments of the quintet of laggard crossovers.

Then who is ahead in this race? No pip count frenzy, please. Just ahead. Only ahead, and perhaps not by how much? A simple question or two: Who is running ahead? When might the doubling cube get involved?

Now imagine a harmonious shift of White’s checkers to impersonate Black’s home board. Then count only the pip differences between those standout black and white checkers.

Look at the board situation below. Can White’s home board look like Black’s by doing some kind of hockey trade? Maybe. Shift the white pair on the 16pt ahead to the 20pt in exchange for the white pair on the 24pt shifted to cover the 22pt and similarly the 23pt spares to cover the 21pt. Same salaries, same pips. With that slight of hand White matches Black’s home board, except for a truant white blot in the outfield. Black has his homebody checker one pip into his home board, gracing the 6pt as yet another spare. Thus Black has a meager one-pip lead in this race. Hardly in range of the doubling cube yet.

It is the same pip count. But are the checkers wisely placed? The game position has a gap-prone home structure for White; the doctored position is as smooth and flexible as Black’s cultured taste. The doctored situation cannot possibly be a cube offer by Black. A single pip ahead in running chances, now the same white home distribution, and nearly a dozen rolls until the last checker is lifted from the board. At a penalty of about $125 in a thousand dollar game, it is a colossal mistake for Black to double the doctored position. But the real game with the white gaps on board, how close is that to a black double? Answer that question and insight into costly gaps will appear. Rollouts confirm that in a cash game the real position is a close Double and easy Take. Not to cube here would ignore about 25mp (0.025 or 25-millipoints) in equity. Rollouts also confirm in the doctored position that the situation is No Double and easy Take by about 125mp (noted above). Hence filling the gapped white home board is worth about one hundred fifty in a thousand.

A second doctored position shifts the white 5pt spare to the 4pt and creates a tally of four crossovers by shifting the white 6pt spare back to pair on the 7pt. See below. Rollouts confirm that this fourth crossover (with deeper 4pt spare) are worth about 30mp per crossover of the previous 125mp, already accounted.

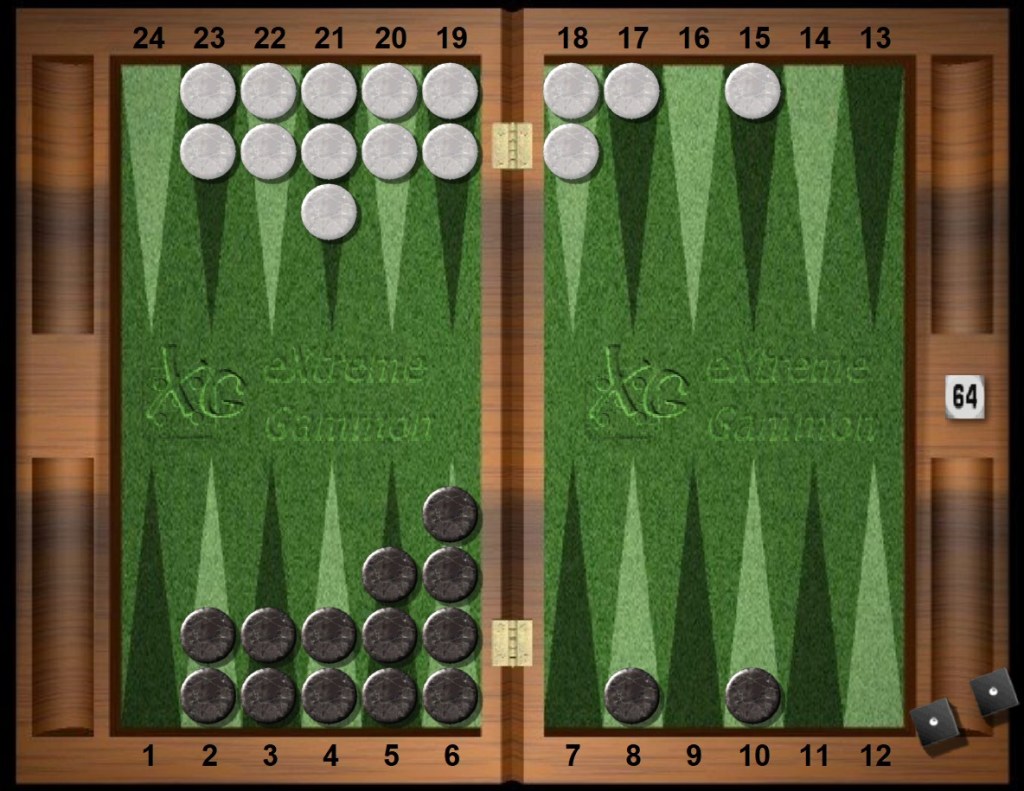
Return to the original position, repeated below. As a cash game cube Black has a first cube (by 25mp), due primarily to White’s gapped home distribution and extra crossovers to delay the first bearoff. White has an easy take, based on only one pip behind.

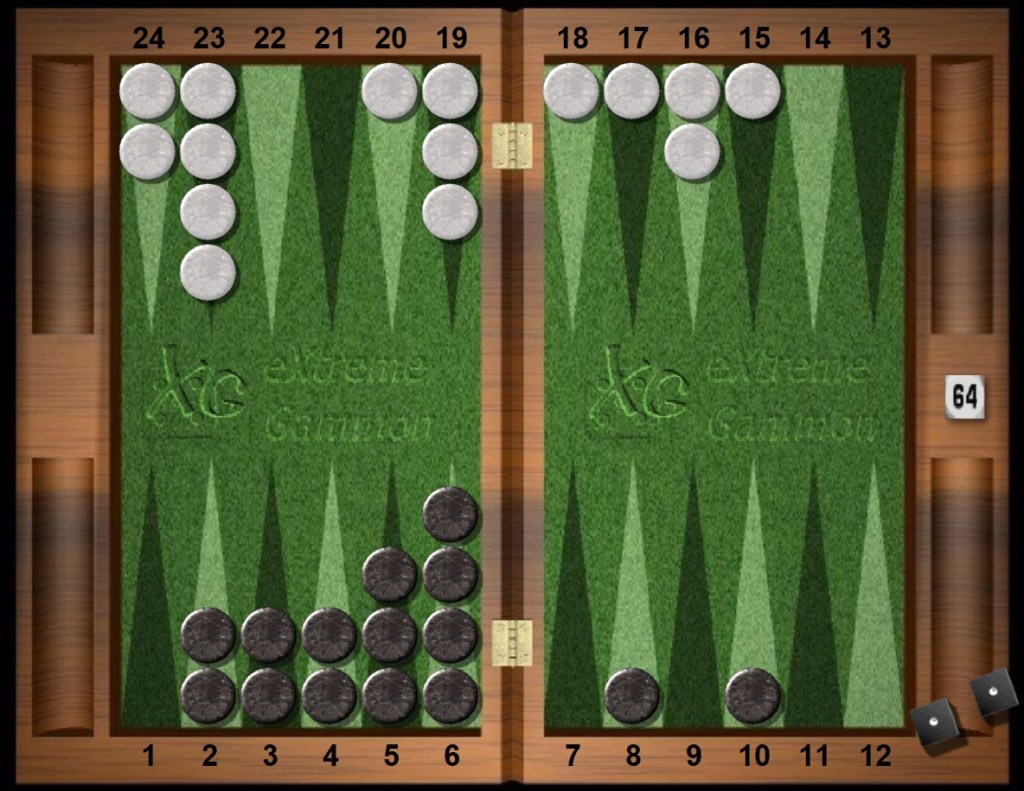
However, Black’s baffled whinge and whistle are partly due to this position occurring at the beginning of a five-point match, and not in a cash game at all. A close cube in a cash game may not be a close cube in a short match. Is a racing lead in a short match more conclusive, or less? Or not different at all?

To recap: First game of a five-point match.  Pure race situation.  Obviously gammons are irrelevant.  Black is on the roll and only leads the race by one pip.  White has five crossovers before starting the bearoff and Black has two crossovers.  White will certainly aim to plug the gaps during the crossovers, so the gaps are likely to be dusted in.  Black has an ace point gap.  The match score is zero-zero in the first game of a five-point match. 

After some research using the bot, this early position at the start of a five-point match, score zero-zero, is rather unusual. Using the KazXG2 MET, all other match scores are doubles. Only in a five-point match is this position a close No Double. Using an XG++ evaluation here is a table:

• 25-point match D/T 0.092% (all XG++)
• 23-point match D/T 0.096%
• 21-point match D/T 0.102%
• 19-point match D/T 0.108%
• 17-point match D/T 0.118%
• 15-point match D/T 0.130%
• 13-point match D/T 0.143%
• 11-point match D/T 0.156%
• 9-point match D/T 0.152%
• 7-point match D/T 0.205%
• 5-point match ND/T -0.144% (actual match conditions)
• 3-point match D/T 0.885%

Moral of the story? Short matches can be very different, both from longer matches and from cash games. Other match equity tables give the following cube actions in this position in a five-point match: KazXG2 ND (0.144%), KRmet ND (0.150%), gnuBG ND (0.111%), XGmet ND (0.063%), Snowie ND (0.082%), JTmet ND (0.064%), Woolsey D 0.027%)

How close are these numbers to a Double? Using the KazXG2 MET, at the outset of a short match, Black seems to have almost a double but not quite.  Accurate rollouts say that Black is 0.121% short in match-winning chances of a double in this position — but how close is that in racing edge?  The pips clearly are the unit of measured size in any pure race.  Thus, to estimate, improve Black’s situation by modifying the pip count by a single pip, first shift the 2pt->1pt, then reset and 5pt->4pt, or 6pt->5pt, or 8pt->7pt, and finally 10pt->9pt.  Thus Black will be two pips ahead in the race, not just one.

Here is a list using the XG++ evaluator.  All except the original position (ND) are correct cubes (D):  Original position: -0.144%, shifted 2pt->1pt: +0.153%, shifted  5pt->4pt: +0.105%, shifted  6pt->5pt: +0.024%, shifted  8pt->7pt: +0.121%, shifted  10pt->9pt: +0.127%.  Notice that all pips are not created equal.  The least sensitive is the stacked 6pt; the most sensitive are the farthest 10pt and the gapped 1pt.  Worth recalling.  One pip closer means about (0.144+0.024) or 1/6 of a percentage point in match-winning chances.

That ought to overdo it!